Volume 5, numéro 2 Université de Montréal Mars 1995
Nigel D. Higson s'est vu attribuer le Prix en raison de la qualité de ses travaux de recherche sur les algèbres d'opérateurs et plus particulièrement la K-théorie algébrique des C*-algèbres. Il a apporté une contribution majeure à la KK-théorie de Kasparov et à la théorie des indices des algèbres d'opérateurs. Professeur Higson a reçu un B.A., une maîtrise et un doctorat de l'Université Dalhousie à Halifax en Nouvelle-Écosse sous la direction du professeur P.A. Fillmore. Après avoir travaillé à l'Université de Pennsylvanie de 1986 à 1990, il s'est joint à l'Université d'état de Pennsylvanie où il occupe aujourd'hui un poste de professeur agrégé. Monsieur Higson a été boursier de la Sloan Foundation.
Michael J. Ward a été honoré pour ses travaux dans le domaine des comportements asymptotiques, de l'informatique appliquée aux calculs scientifiques, et de la modélisation mathématique, plus particulièrement dans le cadre de problèmes physiques. Ses recherches ont trouvé des applications en modélisation d'appareils constitués de semi-conducteurs, théorie de la combustion en régime continu et en diffusion dans des domaines avec des perburbations singulières. Elles ont aussi porté sur des modèles de diffusion-réaction à dynamique interfaciale et comportement métastable, ainsi que sur les hétérogénéités à caractère fortement localisé dont font preuve divers systèmes physiques. Monsieur Ward a reçu un B.Sc. en mathématiques de l'Université de Colombie-Britannique puis un doctorat en mathématiques appliquées de Caltech en 1988, sous la direction de Donald S. Cohen. Après avoir séjourné à l'Université de Stanford et au Courant Institute, il est retourné en 1992 à U.B.C. où il occupe aujourd'hui un poste de professeur adjoint.
Les gagnants ont été choisi par le Comité consultatif du CRM, composé d'une douzaine d'éminents scientifiques canadiens et étrangers.
Le Prix, d'une valeur de 3 000 $, reflète le désir du docteur André Aisenstadt de reconnaître le talent des jeunes chercheurs canadiens en mathématiques.
Les deux récipiendaires présentent un cours résumé de leurs travaux dans le présent numéro du Bulletin.
L'inauguration du symposium a eu lieu à l'auditorium Bell de l'École Polytechnique, le 6 octobre 1994 en présence de Mireille Mathieu (doyenne de la Faculté des arts et des sciences de l'Université de Montréal), Robert Cléroux (doyen de la Faculté des études supérieures de l'Université de Montréal), Christine Martel (présidente du FCAR) et Maurice St-Jacques (vice-recteur de l'Université de Montréal) qui ont signalé à tour de rôle l'importance du CRM dans le développement de la recherche scientifique au Canada.
Les festivités entourant le 25e anniversaire se sont terminées par un banquet sous la présidence d'honneur de Monsieur André Aisenstadt, le samedi soir 8 octobre 1994, à l'Hôtel Ritz-Carlton. Messieurs Maurice L'Abbé , Jacques St-Pierre, Peter Hilton et René Simard y ont prononcé une allocution.
Une publication spéciale dans la série "CRM Proceedings and Lecture Notes", distribuée par l'American Mathematical Society, commémorera ce 25e anniversaire du CRM.
Reported by Martin Goldstein
The Aisenstadt Chair holder, Professor Robert Bryant (Duke) gave a series of five lectures at the CRM in conjunction with the workshop on Exterior Differential Systems in October 1994. He spoke to us over lunch during his visit.
I am from rural North Carolina, I grew up on a farm about thirty miles from the capital city of Raleigh, a town called Kipling of about fifty people in a good year. I hated arithmetic as a kid, just absolutely hated it. It and spelling were my worst subjects, so I had no idea that I would have any interest in mathematics until the summer between my seventh and eighth grades. My uncle dropped out of college and left his books at my grandmother's house, which was just through the woods. I found his college algebra book and his organic chemistry book and they were just fascinating to me. I'd always liked science. As a kid, my parents had gotten me science toys for Christmas or birthdays.
My parents were farmers. Every summer I asked, <<why do they call it summer vacation>>? It was not vacation for me; it was farm work. I looked forward to going back to school because that was easy. It was working on the farm that was annoying. But the summer between seventh and eighth grades, I picked up my uncle's college algebra book and found out that I really liked algebra. It was just fascinating that you could factor polynomials, all these formal manipulations that had some structure and some relation to geometry. Although I did not start studying geometry until much later, I thought computing with geometric figures was neat. However, I never learned to like arithmetic, and to this day my heart sinks when I have to do any real arithmetic. After I finished my uncle's algebra book, I started on his calculus book and I was really excited. The idea that you could calculate the maximum volume of a cylinder inscribed in a sphere, that sort of thing, was the neatest thing I'd ever heard of. The school I went to was quite small. It had about 600 students in all twelve grades. My graduating class had twenty-nine people in it. Because my high school was small, there wasn't any opportunity to take advanced classes, so I didn't really go much beyond calculus until my senior year when I came to the attention of a faculty member at one of the local colleges. He said <<have you studied any differential equations?>> I said <<no, what's that?>> and he said <<do you know any topology?>> I said <<no, what's that?>> To answer my questions, he gave me an armful of books to look at. They had Milnor's knot theory and combinatorics, etc. and were just fascinating. Whenever I got stuck on a problem I could talk to him, since he was at Campbell College, about ten miles away. It was such an exciting year that I almost didn't notice it was my senior year.
There were not really any mathematicians in my family, although my father was very good with figures; he loved arithmetic. He could add a four digit column in his head. It was amazing, and I never saw him make a mistake. But I didn't have any of that talent. I'm the third of six kids. My older brother went to college and became a mathematics teacher. He teaches in the local high school where we grew up, but other than that there wasn't anybody else in the family who was mathematically inclined. I went to college at North Carolina State which is in Raleigh, and I had to go home on the week-ends to farm. My professors saw right away that I had some talent in mathematics and moved me into upper level courses, where I got a lot of stimulation and encountered interesting problems . I actually saw what manifolds were and I liked differential topology. At that time though, I was really enamoured of number theory, and I planned to study analytic number theory in graduate school.
I had a good undergraduate advisor who watched over the courses I took and made sure they were interesting. When I graduated, I went to graduate school at UNC Chapel Hill, which was still in North Carolina but a little bit further from home. I was still going home on week-ends to farm. I stayed at UNC until 1979 when I got my degree, at which point I finally said, <<well I'm not really going to be a farmer>>.
I got my degree in differential geometry. I started in differential topology but midway through graduate school, I began to realize that I liked being able to compute things, so differential geometry was the place to go . Also it was at that time that my advisor introduced me to the works of Elie Cartan, who was a major influence on me because of the beautiful arguments he made and his incredible insight into apparently intractable problems in differential equations and differential geometry. I was really taken with Cartan and I spent a lot of time studying his collected works. I spent a semester in Berkeley, when my advisor, Robby Gardner, went to visit his advisor, S.S. Chern. Chern had been a student of Cartan (more accurately a postdoc), working with him for a year before going back to China. I learned a lot from him about how to read and understand Cartan. That inspired my own thesis work on differential systems. Basically it was a problem in understanding the normal forms of differential systems. What were the best local coordinate systems and what kind of information do they give you? It was also related to what's now known as the cohomology of pseudo-groups. After I finished my thesis, I got a post-doc from the National Science Foundation which allowed me to spend the year 1979-80 at the Institute for Advanced Study. Yau, Rick Schoen, Karen Uhlenbeck, and Leon Simon were all there for a special year in differential geometry, which was ideal for me because I had spent time studying the classical Elie Cartan approach, but I didn't know a lot of modern differential geometry. Spending a year at the Institute where all the people at the forefront of differential geometry were working and giving lectures (Yau was running five lectures and a volleyball game) was great. I didn't write a single paper while I was there, but I learned a lot.
In the summer of 1980, I moved to Rice University for my first job and started working on some problems in differential geometry that I learned about at the Institute, problems in holomorphic curves, CR manifolds, and integral geometry. I hit it off really well with the people at Rice . That was the first time I'd ever lived in a huge city. Houston wasn't really part of the south despite the fact that a lot of people think of it as the south. It's really the southwest, which was a bit of a culture shock for someone having come from a farm in North Carolina. But I liked it a lot more than I thought I would. The city was awash in oil money, and artists and playwrights had moved there along with displaced autoworkers. There was something to do where every; it was really exciting. I was an assistant professor at Rice from 1980 to 1982, when I was promoted to associate and then, two years later, to full professor. In the meantime I had gotten a Sloan fellowship and I was among the first class of Presidential Young Investigators in 1984. I was still working in the geometry of differential equations but I was finding a lot of applications to problems in modern differential geometry. I found it exciting that all this information from the geometry of pde's could be brought to bear on modern global problems. By that time, I had started working with Philip Griffiths, whom I met when Chern had a conference in December 1979. He invited me and Griffiths, who was then at Harvard, to speak. Griffiths was interested in some problems that could be attacked with exterior differential systems and I was interested in algebraic geometry, although I didn't know it at that time. So we traded information and found out that we could make some progress on each others problems. That started our collaboration and we've been working together ever since.
We began writing a book. I guess we really started talking about it at the conference in 1979 but that was sort of pie in the sky stuff. Chern proposed that, with exterior differential systems changing in character and becoming a modern subject, it was time for a modern exposition because there hadn't really been one since Kaehler. That led us to write this book which finally came out in 1991, 12 years later. It was a long process partly because our view of exterior differential systems was changing all the time. We were proving new theorems, seeing new applications of them, and finding that one idea was more important than we thought and another was less important. Our concept of what was to go into the book evolved rapidly throughout those ten years and less than half of what had been envisioned in the beginning was finally published.
I was at Rice until 1987. Griffiths moved to Duke in 1984 and began asking whether I'd be interested in coming back to North Carolina where we could collaborate more closely. We were still working on some interesting problems at the time. I thought about it for a few years and finally made the decision to go to Duke. In North Carolina, the three corners of the research triangle are the universities of State, UNC, and Duke. I've been around the cycle. People ask me, <<when are you going to complete the circuit and move back to State?>> I've been at Duke since 1987 and am still collaborating with Phillip. In fact we recently wrote two-hundred page papers; one is about to appear in the Journal of the AMS and the other in the Duke Mathematics Journal. A third hundred-page paper with Lucas Hsu, a student of mine, has just been finished. We seem to be turning them out pretty rapidly.
I am interested in teaching and I have enjoyed it ever since I started. In fact, while teaching calculus this Fall, I was standing in front of my students about to tell them how things had changed, and I said <<when I first started teaching>> and then paused to reckon up how long it had been. Suddenly I realized that it's been twenty years this Fall that I started teaching as a graduate student. I've always been interested in how to get things across effectively. I don't want to go into a long list of things like awards, but it is something that excites me. I love being in front of students and seeing them go "aha". To see students suddenly realize "oh yeah" is wonderful because at the moment you know that they're thinking the same thing you are and that you're not alone after all. You're not so strange and so different from other people. That contact is very visceral.
I teach about half graduate and half undergraduate classes. I like teaching beginning courses because first-year students have not yet been socialized into being too blasé about the university, so they are still open to being excited in class. Undergraduates, in many ways, can get into a course more than graduate students because it's not yet become a professional thing for them. They're still open to possibilities. In fact, since 1990, I have been associated with the Regional Geometry Institute in Park City, a centre funded by the National Science Foundation. It is a vertically integrated institute that brings together undergraduates, high-school teachers, graduate students, researchers, and so forth for a month every summer. Each year the program is organized around such topics as geometric symmetry and string theory, the geometry of 3-manifolds, and variational principles in pde. There's a research program, a summer school for graduate students, a combination research program-summer school-computer workshop for undergraduates, and a mathematics workshop for high school teachers. All these programs interact. I'm the director of the undergraduate program. The Institute is run by a consortium of universities: Rice University, the University of Chicago, U.T. at Austin, the University of Washington in Seattle, the University of Utah, and Duke. They applied to the National Science Foundation for support for this regional geometry centre. When it first started, I wasn't the director of undergraduate studies. I was invited as a lecturer the first year, then came back the second year because I thought the program was so stimulating. The high school teachers get really excited because they see that geometry was not entirely discovered by the Greeks, and that they are not teaching a dead subject. The undergraduates get excited because they can see what's coming in graduate school and the graduate students get excited because they have access to all those researchers.
It's fun and the setting in Park City (Utah) is perfect for the summer. The atmosphere is very relaxed . The program has now been running for four years, and in the second year they asked me to take over as undergraduate director because I was spending so much time working with the undergraduates . I had a lot of ideas about how to integrate the computer workshop with their courses. The program is not big but we pick the twenty most qualified undergraduates from all over the country and there are some really bright kids. They're already motivated and it's interesting seeing how their undergraduate experience affects their development as mathematicians. The program now has a single institutional sponsor, the Institute for Advanced Study, which is running its administrative structure so it's called the Park City Summer Institute for Advanced Study. The name has gotten much longer but the program is the same, and I'm still the undergraduate director.
I no longer farm. I think I've done enough farming in my life. It's not that I hate it. I just think I've done that. I get all the farming that I want by cutting my grass. I travel. I have been to China six times and travelled around different parts of that country: Inner Mongolia, Chin-Jang, the far flung places. Beijing and Shanghai are interesting because they are the centers of classical Chinese culture and new modernization. However, if you go west to where the national minorities are or north where the Mongolians are, you get a very different sense of what China is like. Of course, it's an enormous country but what people tend to forget is that China is only 80% Han (the ethnic group Han), which leaves 20% of other ethnic peoples, cultures, and languages surrounding the Han center. It has been very interesting visiting those other cultures. Most people think of the non-Han Chinese as Tibetans, but they are only one of a large diversity of minorities. It's fascinating to see all those different cultures coexisting. Chern has an institute, the Nankai Institute at Tanjin, which is about an hour and a half train ride from Beijing. I visit there for a couple of weeks to do mathematics and then spend a week or two travelling in some distant region of China. I've also been to Australia and to Brazil a few times. It is also an exciting place to visit, but I haven't had any dangerous escapes or hair-raising episodes to tell about.
I am not much for organized sports; I used to play some volleyball, but not recently. I run and I work-out. I need the physical exercice. Otherwise I get the jitters and I can't concentrate while sitting at my desk. I bike a lot. North Carolina is great for biking and every week-end that I can, I take a long trip on my bike. Lately, I've been kind of busy. I like music a lot. I'm a very amateur pianist, but I love to try. Like most mathematicians that are into music, I like Bach but I also like some of the late romantics of the early 20th century, like Scriabin. Music plays a big part in my life. I am on the Board of the Chamber Art Society at Duke.
I often listen to music while doing mathematics, although I can't listen to music I'm not familiar with because I find it distracting. Familiar music provides a nice background. It seems to give me energy, that buoyant and positive feeling that you get when you are listening to music. If it is a familiar piece, you can get that feeling without having to concentrate on it or being surprised by the music. You can just flow with it. But when I am listening to a new piece, I have to just stop and listen. I can't think of something else especially if it is modern music. Usually I can't make heads or tails at first of the modern pieces that I often wind up liking. I listen to Arvo Pärt and I like Carter a lot. In mid-century, I like Schoenberg, Ives, and particulary Messiaen. He's really an intriguing composer for me. His Catalogue of the Birds, which is a wonderful cycle of piano pieces, sounds like noise when you first hear it, or it did to me. Maybe to a practiced ear or a professional musician, it would not have sounded so disorganized. I found however that on repeated hearings, it became very compelling. It is really wonderful music but we don't have a context for it like we have for the late romantics or Beethoven because we don't know what to expect next. We haven't heard that much of Messian. It doesn't seem compelling when you first hear it because you are fighting the ideas that are being presented, but I have found that it has come to be among my favorite music. I would love to be able to play his work but it's extremely hard, incredibly hard.
This is my second visit to Montreal. I spoke in the Math department at the Université de Montréal a couple of years ago when I came up to visit Niky Kamran. I was here for a couple of days, not long enough. I think the town is very interesting and, right now, it is really beautiful, but I was speculating that maybe I'd been invited up to Canada to give lectures because I've had so many Canadian students. I have had five Ph.D. students from Canada which must be, among American mathematicians, at the high end. But it has been a wonderful experience. They were great students.
I understand French OK but it's harder for me to speak. I catch about 50% of spoken French in Montréal but reading is no problem since I've spent so much time reading Elie Cartan. My French grammar is OK but my pronunciation may sound pretty strange. It's too bad I couldn't stay for another week or two, particularly now, but I am the director of graduate studies at Duke and I have five graduate students so my time is pretty well taken. Thanks for inviting me up. It's been a great pleasure.
by Michael J. Ward
The scientific focus of my research is physical applied mathematics with an emphasis on modern applications. Physically, I am interested in topics in semiconductor device modeling, steady state combustion theory, diffusion in singularly perturbed regions, interfacial dynamics and metastable behavior in reaction-diffusion models, and the effect of strong localized inhomogeneities in various physical contexts. The mathematical tools used to analyze problems in these areas include singular perturbation and other asymptotic methods, methods from bifurcation theory, and numerical methods. A common theme in the research program is to combine the best features of singular perturbation and numerical methods in order to derive <<tailored>> hybrid asymptotic-numerical methods to treat the nonlinear boundary value problems and partial differential equations arising in the applications. My research to date can essentially be divided into three main areas.
[1] Singularly Perturbed Eigenvalue Problems and Infinite Logarithmic Expansions (Strong Localized Perturbation Theory).
[2] Dynamic Metastability behavior for Reaction-Diffusion Equations and the Analysis of other Singular Perturbation Problems where Exponentially Small Eigenvalues occur.
[3] Mathematical Topics in Semiconductor Device Modeling.
The majority of my co-authored publications, with the notable exception of those written with J.B. Keller (Stanford), have been done with some very talented numerical analysts. They include Luis Reyna (IBM), William Henshaw (Los Alamos, formerly of IBM), Eric Van de Velde (Caltech), Mary-Catherine Kropinski (Courant), June-Yub Lee (Courant).
I will now highlight some of the work in the first two topics.
1. Singularly perturbed Eigenvalue Problems and Logarithmic Expansions
In joint work [21] with Keller, we considered the effect of two types of perturbations of large magnitude but small extent on certain classes of linear eigenvalue problems in a bounded domain D. The types of strong localized perturbations which we considered include the removal of a small subdomain De, of <<radius>> e, from D with the imposition of a condition on the boundary of the resulting hole, and a large alteration of the boundary condition on a small region of the boundary of the domain. For the perturbed problems, the eigenvalues and eingenfunctions were calculated by the method of matched asymptotic expansions for e small. This work provides a significant extension of some previous work by Swanson [18] and by Osawa [13]. The asymptotic results were applied to various problems including certain exit-time problems for Brownian motion.
In joint work with Keller and Van de Velde (see [19], [20]), we have also analyzed similar problems in singularly perturbed geometries for a class of nonlinear eigenvalue problems arising in steady-state combustion theory. The results were applied to determining the change in the conditions for the onset of thermal runaway as a result of the domain perturbation. Mathematically, this involves calculating the corrections to the fold point locations of S-shaped response diagrams in terms of properties associated with the perturbation.
For certain two-dimensional problems with domain perforations, we have shown that the perturbed eigenvalue parameter has an asymptotic expansion that starts with an infinite series in powers of
-1/log[ed(k)], where d(k) is a certain constant characterizing the perturbing subdomain and e is the <<radius>> of the hole. Similar infinite logarithmic expansions have also been obtained for the fold point locations of some two dimensional nonlinear eigenvalue problems In joint work with Henshaw and Keller [22], we have formulated and used a hybrid asymptotic-numerical method to sum these infinite logarithmic expansions. The hybrid results have been favorably compared, at even moderate values of e, with corresponding full numerical results computed from the governing partial differential equations. Our method to treat logarithmic expansions is significant in the sense that logarithmic expansions are generally very slowly convergent (if at all) and thus a finite truncation of the series typically gives poor quantitative agreement unless the small parameter is extremely small.
Our approach to sum infinite logarithmic expansions has also been used in another context. It is well-known from work by Kaplun [7] and Proudman and Pearson [14] that an infinite logarithmic expansion arises in the classical fluid mechanics problem of calculating the drag coefficient of a cylindrical body in a low Reynolds number fluid flow. A three-term truncation of the infinite logarithmic expansion is well-known to provide a rather poor determination of the actual drag coefficient at low Reynolds number. Furthermore, it is intractable analytically to compute further terms in the expansion. In joint work with Kropinski and Keller [10], we have solved this long-standing problem by formulating analytically and implementing numerically a hybrid asymptotic-numerical method that sums the infinite logarithmic expansion for the drag coefficient. The hybrid results have been favorably compared with corresponding experimental and full numerical results over a range of low Reynolds number flows.
2. Singular Perturbation Problems with Exponentially Small Eigenvalues
In general terms, the work under this heading represents our contribution to some of the recent activity in the growing field of exponential asymptotics. We now describe some of the problems and the results obtained.
There are certain classes of singularly perturbed boundary value problems where a straight-forward application of the method of matched asymptotic expansions (MMAE) fails to determine the solution uniquely. Two classes of such problems are the linear turning point problems exhibiting the phenomena of boundary layer resonance (see [1], [5]), and certain nonlinear autonomous two-point boundary value problems with internal layer solutions (see [11], [18]). The unifying link between these various problems is the occurrence, in one way or another, of exponentially small eigenvalues. This exponential ill-conditioning clearly indicates that the solutions to these problems are sensitive to small perturbations and are very difficult to compute numerically.
For the nonlinear internal layer problems the internal layer locations are difficult to determine using a traditional MMAE approach. To resolve this indeterminacy in the internal layer locations, two previous methods have been proposed and used on a few special examples: an extension of MMAE to explicitly match the crucial exponentially small terms [11]; a method based on a variational principle, [8]. Recently, I have given two new methods to determine the internal layer locations that can be used for various classes of nonlinearities. The first method, which is called the projection method ([23]), is based on combining the MMAE approach with the fact that the linearized problem about the MMAE solution is exponentially ill-conditioned. The projection method is motivated by the work of [5] for linear problems and by an observation in [8]. The second method, introduced in [16], applies to certain classes of nonlinearities and is based on a preliminary WKB-type nonlinear change of variables. The main advantage of the WKB method is that the need for exponential asymptotics is eliminated, and thus exponentially sensitive steady-state internal layer solutions are readily computed numerically. In [12], a related projection method is to construct high order asymptotic solutions to some exponentially ill-conditioned linear turning point problems and the asymptotic results were verified numerically.
Some of the problems described above arise as the steady-state solutions to certain time-dependent mathematical models of phase separation of a binary mixture. Examples of such phase separation models include the Allen-Cahn equation [4], [6] and the fourth-order Cahn-Hilliard equation [3], [2]. The Cahn-Hilliard equation is a continuum model for spatial pattern formation that occurs when certain mixable binary mixtures are cooled to below some critical temperature. The internal layer patterns that are formed are not stable in the strict sense but do typically persist over very long time intervals. This phenomenon of dynamic metastability for spatial patterns occurs in many of these phase separation models. The exponentially small eigenvalues alluded to above are directly responsible for this behavior. For these phase separation models our goal has been to characterize the metastable behavior and to quantify the coarsening process, which describes the process of annihilation of internal layers leading eventually to a stable pattern.
The Allan-Cahn equation is the simplest model for such slow phase separation. In previous work of [4] and [6], the dynamic metastability phenomenon was analyzed for the Neumann problem. In [24], the projection method was used to extend this work to other nonlinearities and boundary conditions. In addition, a hybrid asymptotic-numerical method was formulated and implemented to quantify the coarsening process. In [16], dynamic metastability results were obtained for a variant of the Allen-Cahn equation, called the constrained Allen-Cahn equation, where mass is conserved. The WKB method was also used to compute the metastable phenomena over very long time intervals. Finally, in [15], the projection method is used to derive equations of motion for the internal layer locations associated with metastable patterns in the Cahn-Hilliard equations and some extensions. A high order and accurate finite-difference method was used to verify the analytical results. Further work in characterizing dynamic metastability phenomena in other situations, including applications in more than one spatial dimension, is in progress.
Exponentially small eigenvalues also occur for other diffusion problems in the small diffusivity limit. For example, in [17] we used the WKB method and the projection method to analyze internal layer phenomena for a class of viscous shock problems where the linearized operator has an exponentially small eigenvalue. This work was motivated by the numerical study of [9] for the initial boundary value problem for Burgers equation. For this class of problems we showed that the viscous shock motion is exponentially slow and we used the WKB method to accurately compute exponentially sensitive steady state solutions and to track the viscous shock layer motion over very long time intervals. The WKB method also reveals a very striking analogy between the viscous shock problem and the Allen-Cahn model of phase separation.
REFERENCES
[1] R. Ackerberg, R.E. O'Malley, Boundary Layer Problems Exhibiting Resonance, Studies in Appl. Math. 49, (1970), pp. 277-295.
[2] N. Alikakos, P.W. Bates, N. Fusco, Slow Motion for the Cahn-Hilliard Equation in One Space Dimension, J. Differ. Equations 90, (1991), pp. 81-135.
[3] J. Cahn, J. Hilliard, Free Energy of a Non-Uniform System. I. Interfacial Free Energy, J. Chem. Phys. 28, (1958), pp. 258-267.
[4] J. Carr, R. Pego, Metastable Patterns in Solutions of ut=e2uxx=e2uxx-f(u), Comm. Pure Appl. Math. 42, (1989), pp. 523-576.
[5] P.P.N. De Groen, The Nature of Resonance in a Singular Perturbation Problem of Turning Point Type, SIAM J. Math. Anal. 11, (1980), pp. 1-22.
[6] G. Fusco, J. Hale, Slow Motion Manifold, Dormant Instability and Singular Perturbation, J. Dynamics and Diff. Equations 1, (1989), pp. 75-94.
[7] S. Kaplunn, Low Reynolds Number Flow Past a Circular Cylinder, J. Math. Mech. Vol. 6, No. 5, (1957), pp. 52-60.
[8] W. Kath, C. Knessl, B. Matkowsky, A Variational Approach to Nonlinear Singularly Perturbed Boundary Value Problems, Studies in Appl. Math. 77, (1987), pp. 61-88.
[9] G. Kreiss, H. Kreiss, Convergence to Steady State of Solutions of Burgers Equation, Appl. Numerical Math. 2, (1986), pp. 161-179.
[10] M.C. Kropinski, M.J. Ward, J.B. Keller, A Hybrid Asymptomatic-Numerical Method for Calculating Low Reynolds Number Flows Past Symmetric Cylindrical Bodies, accepted SIAM J. Appl. Math. 11/94.
[11] C. Lange, On Spurious Solutions of Singular Perturbation Problems, Studies in Appl. Math. 68, (1983), pp. 227-257.
[12] J.Y. Lee, M.J. Ward, On the Asymptotic and Numerical Analysis of Exponentially Ill-Conditioned Singularly Perturbed Boundary Value Problems, to appear, Studies in Appl. Math. 5/94.
[13] S. Ozawa, J. Fac. Sci. Univ. Tokyo Sec. IA 30 (1983), pp. 243-257; J. Fac. Sci. Univ. Tokyo Sec. IA 30 (1983), pp. 259-277; J. Fac. Sci. Univ. Tokyo Sec. IA 30 (1983), pp. 53-62; Duke Math. J. 48 (1981), pp. 767-778.
[14] J. Proudman, J. Pearson, Expansions at Small Reynolds Number for the Flow Past a Sphere and a Circular Cylinder, J. Fluid Mech. 2, (1957), pp. 237-262.
[15] L.G. Reyna, M.J. Ward, Metastable Internal Layer Dynamics for the Viscous Cahn-Hilliard Equation, in revision, Methods and Applications of Analysis 11/94.
[16] L.G. Reyna, M.J. Ward, Resolving Weak Internal Layer Interactions for the Ginzburg-Landau Equation, to appear, European J. Appl. Math. 12/94.
[17] L.G. Reyna, M.J. Ward, On the Exponentially Slow Motion of a Viscous Shock, to appear, Comm. Pure Appl. Math. 1/95.
[18] C. Swanson, Asymptotic Variational Formulae for Eigenvalues, Canadian Math. Bull. 6 (1963), pp. 15-25.
[19] M.J. Ward, J.B. Keller, Nonlinear Eigenvalue Problems under Strong Localized Perturbations with applications to Chemical Reactors, Studies in Appl. Math. Vol. 85 No. 1, (1991), pp. 1-28.
[20] M.J. Ward, E. Van De Velde, The Onset of Thermal Runaway in Partially Insulated or Cooled Reactors, IMA J. Appl. Math. Vol. 48 No. 1 (1992), pp. 53-85.
[21] M.J. Ward, J.B. Keller, Strong Localized Perturbations of Eigenvalue Problems, SIAM J. Appl. Math. Vol. 53 No. 3, (1993), pp. 770-798.
[22] M.J. Ward, W.D. Henshaw, J.B. Keller, Summing Logarithmic Expansions for Singularly Perturbed Eigenvalue Problems, SIAM J. Appl. Math. Vol. 53 No. 3, (1993), pp. 799-828.
[23] M.J. Ward, Eliminating Indeterminacy in Singularly Perturbed Boundary Value Problems with Translation Invariant Potentials, Studies in Appl. Math. Vol. 87 No. 2, (1992), pp. 95-135.
[24] M.J. Ward, Metastable Patterns, Layer Collapses, and Coarsening for a One-Dimensional Ginzburg-Landau Equation, Studies in Appl. Math. Vol. 91 No. 1, (1994), pp. 51-93.
par Ghislain Giroux-Dufort
Robert Lacroix, président- directeur général du CIRANO, et Luc Vinet, directeur du CRM, ont signé, le 23 décembre 1994, un protocole d'accord visant à établir un partenariat de recherche et de transfert en finance mathématique et en statistique de la finance.
Le premier programme conjoint issu de ce nouveau partenariat s'inscrira dans le cadre de l'année thématique du CRM consacrée à l'analyse numérique et appliquée. Il consistera en une série de conférences sur la finance mathématique (décembre 1995 - janvier 1996), suivies d'un atelier sur le même sujet (mai 1996). Le professeur Ioannis Karatzas, de la Columbia University, sera titulaire de la Chaire Aisenstadt du CRM durant cette période. Le comité scientifique consultatif de ce programme est constitué de: Luis Cafferelli (Institute for Advanced Study), J. Darrell Duffie (Stanford University), Ioannis Karatzas (Columbia University) et Stanley Pliska University (University of Illinois at Chicago). (De plus amples détails sur ce programme et les autres conférenciers qui y participeront suivront au cours de l'année.)
Le CIRANO (Centre interuniversitaire de recherche en analyse des organisations) est un centre de liaison et de transfert établi à Montréal et regroupant des chercheurs de premier plan de six institutions universitaires du Québec. Sa mission vise non seulement l'avancement des connaissances dans le domaine de l'analyse scientifique des organisations et des comportements stratégiques, mais aussi leur diffusion dans les milieux d'application. Les chercheurs du CIRANO font une utilisation intensive des mathématiques et de la statistique avancées dans leurs recherches théoriques et appliquées.
Nos lecteurs savent que le CRM est un centre national de recherches ayant pour mission de contribuer au développement des sciences mathématiques dans leur ensemble. À cette fin, il poursuit des travaux de recherche, organise des programmes thématiques et divers événements scientifiques, et édite des monographies et des comptes rendus. Tout en poursuivant ses activités actuelles, le CRM entend exercer son leadership pour stimuler le développement de nouveaux axes de recherche prometteurs. Il souhaite entre autres développer des programmes de recherche avec le secteur privé, en particulier dans le domaine des finances mathématiques et de la statistique de la finance.
C'est dans ce contexte que le CIRANO et le CRM ont convenu de collaborer. Outre l'organisation de conférences telles qu'annoncées ci-haut, les activités envisagées sont l'établissement de projets de recherche conjoints, la création ou la contribution à des postes, des bourses de recherche, des activités scientifiques, des publications, etc.
Dans le but de faciliter l'établissement, le financement et la gestion des activités envisagées dans le cadre de ce partenariat, le CIRANO et le CRM ont formé un comité de gestion constitué de quatre membres: Jérôme Detemple (CIRANO, Université McGill), Eric Ghysels (CIRANO, Université de Montréal), Daniel Dufresne (CRM, Université de Montréal), et Martin Goldstein (CRM, Université de Montréal).
N'hésitez pas à communiquer avec le CRM (CRM@ERE.UMontreal.CA) pour tout renseignement sur cette nouvelle association ou pour formuler des suggestions ou projets de recherche qui puissent s'inscrire dans le cadre de ce partenariat.
by Nigel D. Higson
The following is a brief description of the research interests of Dr. Nigel D. Higson, recipient of the Aisenstadt Prize.
In the following paragraphs I have tried to give a quick overview of the general area of my research, ending with one problem of current interest to me.
A C*-algebra is a Banach *-algebra which is isomorphic to a norm-closed, *-subalgebra of the algebra of all bounded operators on a Hilbert space. Important examples are:
The K-theory groups of C*-algebra are the homotopy groups of its stable general linear group:
The Bott Periodicity Theorem asserts that
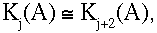
and we use this to define Kj(A) for all j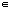 
Z, in such a way that
periodicity continues to hold. We obtain a sort of "homology theory" on the
category of C*-algebras. For instance if J is a closed, two-sided ideal in A
then there is a periodic long exact sequence
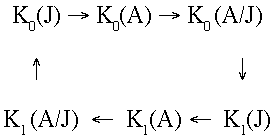
analogous to the long exact sequence in cohomology theory.
The K-theory groups of the commutative C*-algebra C0(X) identify with the Atiyah-Hirzebruch K-theory groups of the space X.
Suppose, for instance, that G is a locally compact abelian group. Then the structure of C*r(G) is readily described by the Fourier transform, which provides an isomorphism between C*r(G) and the algebra C0 (G) of continuous functions on the Pontrjagin dual of G which vanish at infinity. The K-theory groups Kj(Cr*(G)) identify with the Atiyah-Hirzebruch K-theory groups of the locally compact space G,
(1)
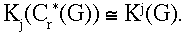
If G is non-abelian then the theory of the Fourier transform is not so simple, but it has nonetheless proved useful to think of C*r(G) as being <<dual>> to a space of irreducible representations of G, in the same sense that C0(X) is dual to X. This leads to the notion that the groups Kj(Cr*(G)) represent the K-cohomology of this dual space of representations. For instance, if G is a complex semisimple group then K*(Cr*(G)) identifies with the Atiyah-Hirzebruch K-theory of the tempered dual of G (which turns out to be a Hausdorff locally compact space). But on the other hand if G is the free group on two generators then the groups Kj(Cr*(G)) have no counterpart in ordinary topology. In both cases, the groups K*(Cr*(G)) play an important role in problems which address the topology of representations of G.
The Baum-Connes Conjecture
Paul Baum and Alain Connes have proposed a means of calculating the groups Kj(Cr*(G)) which blends group homology with the representation theory of compact subgroups of G. The conjecture, if true, would have a number of implications in geometry and topology, as well as C*-algebra theory. In addition there are close connections with the tempered representation theory of Lie groups and p-adic groups.
The formulation of the conjecture uses Kasparov's KK-theory [5]. Following Atiyah, Kasparov formalized a notion of abstract elliptic operator D on a locally compact space X and assembled the collection of all elliptic operators on X into K-homology groups Kj(X). If X is compact then each abstract elliptic operator on X has a Fredholm index:
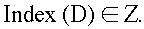
If X is locally compact but admits a proper G-action, with G\X compact, and if D is G-equavariant, then D has an equivariant index
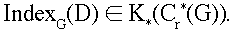
(If G is the trivial group then K*(Cr*(G)) @ Z, and the equivariant index reduces to the ordinary one.) The Baum-Connes conjecture asserts that K*(Cr*(G)) is generated by these indices, and furthermore that the only relations among them are those imposed from simple geometric considerations. To be a little more precise, the set of all operators like D is organized into a group, called K*G(EG) in the paper [1], and the Baum-Connes conjecture is that
(2)
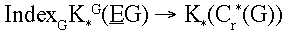
is an isomorphism.
For various classes of groups the conjecture assumes a much simpler form which does not involve Kasparov's theory. This leads to various interpretations special cases:
If G is semisimple Lie group then each discrete series representation is an isolated point in the tempered dual and contributes a generator to the abelian group K0(Cr*(G)). For these K-theory classes, the conjecture is closely related to the problem of geometrically realizing discrete series representations. If G is a reductive p-adic group the conjecture is closely related to the problem of realizing supercuspidal representations as induced from compact open subgroups.
Asymptomatic Morphisms and Deformations of C*-Algebras
Kasparov's KK-theory is a sort of bivariant homology/cohomology theory on the category of (separable) C*-algebras. Alain Connes and I have introduced a new bivariant theory, based on the following idea [2,3]:
Definition. Let A and B be C*-algebras. An asymptotic morphism from A to B is a family of functions
such that jt(a) is continuous in t and
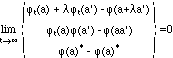
for all a, a' 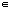A and l 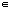C.
The definition has these important features
* An asymptotic morphism jt:A Æ B induces a homomorphism of K-theory groups j:A Æ B.
* After suitable reparametrizations, asymptotic morphisms may be composed in a manner which generalizes the composition of ordinary homomorphisms.
* Asymptotic morphisms A Æ B correspond to deformations of the C*-algebra A into B.
Roughly speaking, we assemble the asymptotic morphisms from A to B into a group E(A,B) which is analogous to Kasparov's KK(A,B). Composition of asymptotic morphisms gives the product operation which is central to Kasparaov's theory.
As an illustration of E-theory, here is a reinterpretation of the Baum-Connes conjecture in the case of a connected Lie group G (in which case the conjecture is usually referred to as the Connes-Kasparov conjecture). Let H be a maximal compact subgroup of G, and form the semidirect product Lie group
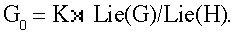
There is a natural smooth family of Lie groups Gt interpolating between G0 and G1 = G, in which all Gt for t > 0 are isomorphic to G1 by a change of scale. (This is called the contraction of G along H in the mathematical physics literature.) The field of C*-algebras C*r(Gt) is a deformation of the sort mentioned above.
Conjecture. The field of C*-algebras C*r(Gt) has constant K-theory. Equivalently, the asymptotic morphism associated to this C*-algebra deformation induces an isomorphism on K-theory groups K*(Cr*(G0)) @ (Cr*(G1)).
It is interesting to calculate this continuous field in various cases. If G is a complex semisimple group then one can show that the field is assembled from constant fields by extensions and Morita equivalences [4]. This implies that our deformation is constant at the level of K-theory, but it also goes quite a bit further. In terms of representation theory it says that the classification of (tempered) irreducible unitary representations by <<lowest K-type>> is the same for all Gt. As far as I can tell, this fact - which appear to hold good for real semisimple groups, and gives an interesting <<explanation>> for the structure of the tempered dual - has gone unnoticed in the representation theory literature.
REFERENCES
[1] P. Baum, A. Connes and N. Higson, Classifying space for proper actions and K-theory for group C*-algebras, Contemp. Math. 167 (1994), 241-291.
[2] A. Connes, Non Commutative Geometry, Academic Press, 1994.
[3] A. Connes and N. Higson, Déformations, morphismes asymptotiques et K-théorie bivariante, C.R. Acad. Sci. Paris 311 Série 1 (1990), 101-106.
[4] N. Higson, Deformations of C*-algebra and the Connes-Kasparov conjecture for complex semisimple groups, Preprint.
[5] G.G. Kasparov, Operator K-theory and its applications: elliptic operators, group representations, higher signatures, C*-extensions, Proc. Internat. Congress of Mathematicians, vol 2, Warsaw, 1983, pp. 987-1000.
![[Panneau principal CRM]](/Graphic/HomeFrancais.gif)
![[CRM Home Page]](/Graphic/HomeEnglish.gif)